Eficiencia, Espacio y Tiempo

Cuando hablamos de estructuras de datos o algoritmos, eficiencia se refiere a qué tan bien utilizan los recursos computacionales (como tiempo y memoria). Evaluar la eficiencia nos permite tomar decisiones informadas sobre qué estructura o algoritmo es el más adecuado para una tarea específica.

Complejidad temporal (tiempo)

La complejidad temporal indica cuánto tarda un algoritmo en ejecutarse, según la cantidad de datos de entrada (n). Se expresa usando la notación Big O:

Notación	Ejemplo de algoritmo	Descripción
O(1)	Acceso directo a un arreglo	Tiempo constante
O(log n)	Búsqueda binaria	Tiempo logarítmico
O(n)	Recorrido de una lista	Tiempo lineal
O(n log n)	Merge sort	Tiempo subcuadrático
O(n^2)	Burbujas (Bubble Sort)	Tiempo cuadrático

Complejidad espacial (espacio)

La complejidad espacial analiza la cantidad de memoria adicional que un algoritmo necesita. Por ejemplo:

• Guardar datos temporales o estructuras auxiliares (pilas, tablas)
• Uso de recursión, donde cada llamada consume memoria de pila.

"Evaluar tanto el tiempo de ejecución como el consumo de memoria es esencial para sistemas donde los recursos son limitados o el rendimiento es crítico" (Sedgewick & Wayne, 2011).

Aplicaciones prácticas

Escenario	Relevancia de análisis de eficiencia
Juegos en línea	Tiempo de respuesta en tiempo real
Motores de búsqueda	Optimizar búsquedas en grandes volúmenes
Dispositivos móviles	Uso eficiente de memoria limitada
Inteligencia artificial	Procesamiento rápido de grandes datasets

Representación visual

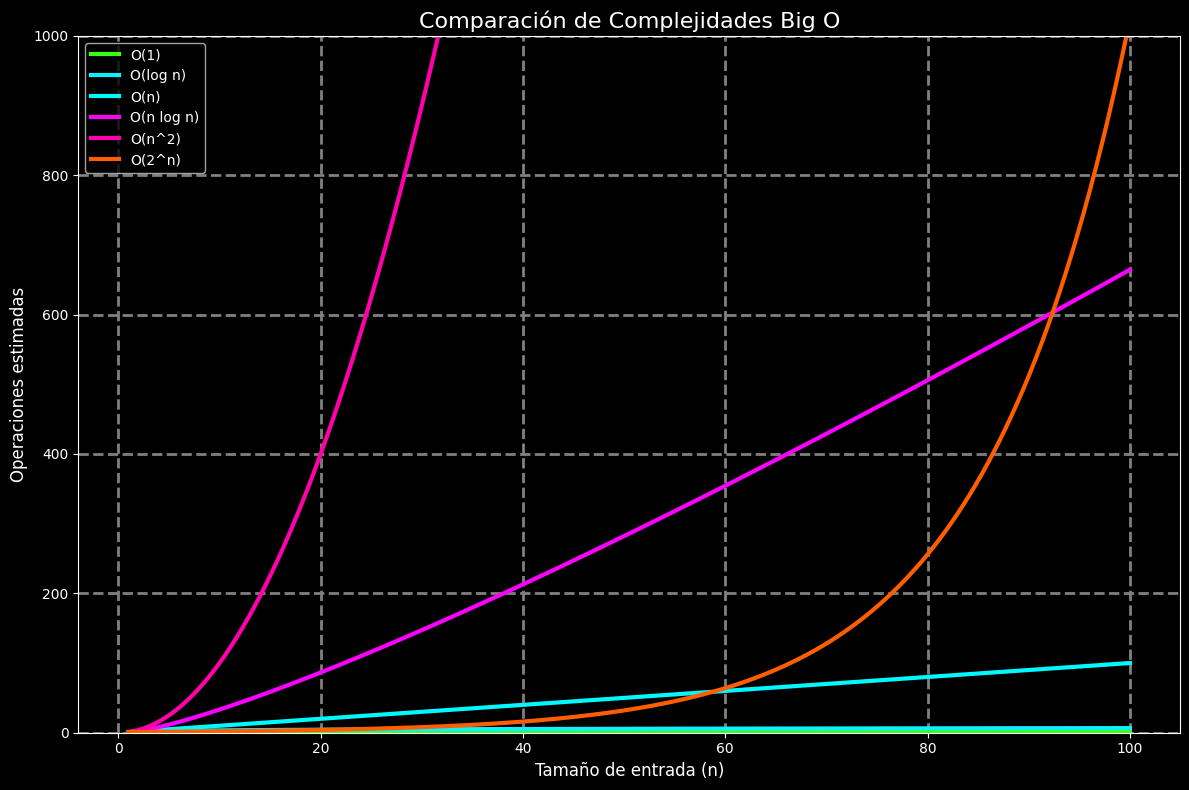
Comparación de tiempos de ejecución teóricos

Input (n) → █ Tiempo

O(1):      █
O(log n):  ███
O(n):      ███████
O(n log n):███████████
O(n²):     █████████████████

Ejemplos

Paradigma: Orientado a Objetos

Código Java Ejemplo

TimeSpaceAnalyzer.java

import java.util.ArrayList;
import java.util.List;

public class TimeSpaceAnalyzer {
    public static int sumLinear(List<Integer> list) {
        int total = 0;

        for (int num : list) {
        total += num;
        }

        return total;
    }

    public static int[][] createMatrix(int n) {
        return new int[n][n]; // Espacio O(n^2)
    }
}

Test Unitario

TimeSpaceAnalyzerTest.java

import org.junit.jupiter.api.Test;
import java.util.Arrays;
import static org.junit.jupiter.api.Assertions.*;

class TimeSpaceAnalyzerTest {
    @Test
    void testSumLinear() {
        var list = Arrays.asList(1, 2, 3, 4);
        assertEquals(10, TimeSpaceAnalyzer.sumLinear(list));
    }

    @Test
    void testCreateMatrixSize() {
        int[][] matrix = TimeSpaceAnalyzer.createMatrix(3);
        assertEquals(3, matrix.length)
    }
}

Paradigma: Procedural

Código Python Ejemplo

efficiency.py

def factorial(n):
    if n == 0 or n == 1:
        return 1
    return n * factorial(n - 1)

def memory_heavy_list(n):
    return [[0]*n for _ in range(n)] # Espacio O(n^2)

Test Unitario

test_efficiency.py

import unittest
from efficiency import factorial, memory_heavy_list

class TestEfficiency(unittest.TestCase):
    def test_factorial(self):
        self.assertEquals(factorial(5), 120)

    def test_memory_heavy(self):
        mat = memory_heavy_list(4)
        self.assertEquals(len(mat), 4)

if __name__ == "__main__":
    unittest.main()

Paradigma: Funcional

Código TypeScript Ejemplo

binarySearch.ts

export const binarySearch = (arr: number[], target: number): number => {
    let left = 0, right = arr.length - 1;

    while (left <= right) {
        const mid = Math.floor((left + right) / 2);
        if (arr[mid] === target) return mid;
        arr[mid] < target ? left = mid + 1 : right = mid - 1;
    }

    return -1;
}

Test Unitario

binarySearch.test.ts

import { binarySearch } from "./binarySearch";

test("binarySearch finds index", () => {
    const array = [1, 3, 5, 7, 9]
    expect(binarySearch(array, 5)).toBe(2);
});

test("binarySearch not found", () => {
    expect(binarySearch([1, 2, 3], 10)).toBe(-1);
});

Referencias

• Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2022). Introduction to Algorithms (4.ª ed.). MIT Press.
• Sedgewick, R., & Wayne, K. (2011). Algorithms (4.ª ed.). Addison-Wesley.
• Python Software Foundation. (2024).
• Oracle Java Documentation. (2024).
• TypeScript Handbook. (2024).